История практического решения Задачи максимального потока минимальной стоимости.
Модель ГТС

В один прекрасный рабочий день 20.. года отцами основателями компании была сформулирована задача моделирования газотранспортной системы.
Требования были сравнительно мягкие, т.е. с приблизительной точностью нужно определить, дойдет ли газ от мест добычи до мест потребления. Если максимальный поток меньше объема добычи или потребления, значит где-то прячется в наших представлениях о ГТС ошибка.
Для уточнения экспертных оценок и проверки этих самых исходных данных. Так как очевидно, что если газ, например, потреблен в течение года, то его добыли и прокачали по магистралям. Пропускная способность магистралей, сведения о добыче газа и его потребления собирались из открытых источников.
Исходные данные были собраны в таблицы Excel, в столбцах по годам.
Первая попытка

Для решения задачи выбрали заслуженную программу Maple. Макрос в Excel 2003 выгружал данные о транспортной сети в текстовые файлики в подходящем для Maple формате.
Maple честно рассчитывал максимальный поток и выдавал результат в виде колонок чисел. Транспортная сеть модели насчитывала не более 60 узлов.
Вторая попытка
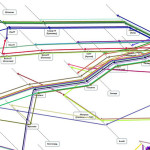
Задумались, как все это отобразить в удобном виде схемы потоков на транспортной сети. Хорошая визуализация позволяет увидеть ошибки подготовки данных, ошибки в работе алгоритма.
Алгоритм решения Задачи максимального потока нашелся в книге Стивенса Рода (1). Код, написанный на Visual Basic, был с минимальными усилиями перенесен в Excel. Дополнительно написаны процедуры загрузки данных в формат алгоритма и отрисовки карт с отображением загрузки магистралей. Получилось круто!
Все особенности «приручения» математических алгоритмов для прикладных задач описаны, например, в Википедии (Обобщения, сводящиеся к исходной задаче). Многочисленные источники с известным ресурсом (мощностью) превращаются в ребра такой-же пропускной способности, подключенные к Истоку. Аналогично поступаем с потребителями.
До идеала еще далеко
Программа заработала, алгоритм (на мой взгляд, ближе всего к Динцу) работал быстро и идеально точно. Схема рисовалась. Можно контролировать процесс и вставлять картинки в презентации с минимальной доработкой.
Быстро выяснилось, что алгоритм ищет кратчайший по количеству пройденных ребер путь от Истока до Стока, причем маршрут зависит от порядка загрузки ребер в массив в случае, если количество ребер в аугментальном пути одинаковое. Т.е. только максимальный поток и никаких оптимизаций. Также в практике существующих газотранспортных сетей используются магистрали с возможностью реверса (редко) и без него (часто). Такая же ситуация на московских центральных улицах и переулках.
Нужно было реализовать возможность указывать эту особенность для магистралей в наших исходных данных. Если вопрос с реверсом был решен доработкой алгоритма сравнительно быстро, то выбор и отладка алгоритма для оптимизации по расстоянию (указанным весам ребер) заняла много времени.
Обидно, что известные с 70-ых и ранее годов прошлого века наработки не так просто, оказывается, кодить. Причем ошибки кода вылезают не сразу, а уже на «горячей» модели.
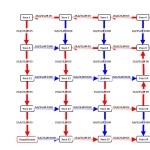
Часто бывало, что на простой и наглядной схеме ошибок нет, а на схеме с сотней и более узлов ошибку оптимизации не видно, и обнаружить ее можно лишь случайно. Или пересчитав исходную сеть заведомо верным алгоритмом. Для отладки использовались как численные логи, отражающие ход расчета, так и графические, рисующие аугментальные пути, найденные алгоритмом.
Релаксация
Приятное такое слово и простое описание алгоритма Беллмана-Форда (1969). Позволяет найти кратчайший путь в транспортной сети не по банальному количеству пройденных ребер, а по их весу. На практике удалось его запустить не сразу, и работает заметно медленней простого расчета максимального потока. Так как ошибок расчета на десятке тестовых схем найти не удалось, считаю, что все работает правильно.
Графическая часть также обросла разными удобствами.
Перспектива
Интересно было бы научить программу решать такие подзадачи:
- равномерная загрузка магистралей. Если есть варианты маршрутов потока, распределить этот поток по свободным магистралям равномерно, сохраняя размер потока
- строить зависимость стоимости потока от его размера. Предположим, мы уменьшили поставки на 10% а получили уменьшение стоимости транспорта единицы продукции на 5%.
Краткое описание инструмента и возможность скачать таблицы с рабочими алгоритмами тут.
Использовались статьи и книги
- Стивенс Род «Готовые алгоритмы на Visual Basic» (1998)
- Седжвик Р. «Фундаментальные алгоритмы на C++», Часть 5 «Алгоритмы на графах» (2002)
- Максимальный поток минимальной стоимости http://habrahabr.ru/post/61884/ (2009)
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. «Алгоритмы: построение и анализ» ( Thomas H Cormen, Introduction to Algorithms) (2005)